[03. 패키지 - SymPy] (1) 기본 함수, (2) 미분방정식(sy.dsolve), (3) (연립)방정식(sy.solve)
작성자 : kim2kie
(2023-02-19)
조회수 : 10615
SymPy는 변수를 심볼로 지정한 문자 연산이 가능하다.
Jupyter를 사용하여 웹에서 보기 쉽게 (LaTex로) 심볼을 나타낼 수 있다.
(1) 기본 함수
(2) 미분방정식(dsolve)
1) 2계 미분방정식(사용법)
2) 2계 미분방정식(Matlab과 결과 그래프 비교)
(3) (연립)방정식(solve)
(1) 기본 함수
import sympy as sy
Ex) simplify() 간략하게
x = sy.symbols('x')
expr=2*x+3*x-sy.sin(x)-3*x+42
sy.simplify(expr)
결과: 2*x - sin(x) + 42
Ex) factor() 인수분해
sy.factor(x**2-2*x-8)
결과: (x - 4)*(x + 2)
Ex) expand() 전개
sy.expand((x-4)*(x+2))
결과: x**2 - 2*x - 8
Ex) collect(,x) x에 대해 정리
m,n = sy.symbols("m,n")
sy.collect(x**2+x*m+n*x+m*n, x)
결과: m*n + x**2 + x*(m + n)
Ex) subs() 수식에 숫자 대입
y = sy.symbols('y')
expr = sy.sin(x) + sy.cos(y)
expr.subs({x:1, y:2})
결과: cos(2) + sin(1)
expr.subs({x:1, y:2}).n()
결과: 0.425324148260754
Ex) 삼각함수
sy.sin(sy.pi/6)
결과: 1/2
sy.cos(sy.pi/6)
결과: sqrt(3)/2
sy.expand_trig(sy.sin(2*x))
결과: 2*sin(x)*cos(x)
Ex) 복소수
from sympy import I
I*I
결과: -1
z=4+3*I
sy.re(z)
결과: 4
sy.im(z)
결과:3
sy.Abs(z)
결과: 5
sy.arg(z)
결과: atan(3/4)
sy.conjugate(z)
결과: 4 - 3*I
Ex) 미분
sy.diff(x**3, x) # 1계 미분
결과: 3*x**2
sy.diff(x**2*sy.sin(x), x)
결과: x**2*cos(x) + 2*x*sin(x)
sy.diff(x**3, x, 2) # 2계 미분
결과: 6*x
Ex) 적분
sy.integrate(x**3, x)
결과: x**4/4
sy.integrate(sy.sin(x), x)
결과: -cos(x)
sy.integrate(sy.ln(x), x)
결과: x*log(x) - x
sy.integrate(x**3, (x, 0, 1))
결과: 1/4
(2) 미분방정식
1) 2계 미분방정식(사용법)
미분방정식(ode): y" + 3y - 1 = 0
초기 조건(ics): y(1)=2
초기 조건(ics): y(0)=0, y'(0)=0
Ex)
import sympy as sy
x = sy.symbols('x')
f = sy.symbols('f',cls=sy.Function)
y = f(x)
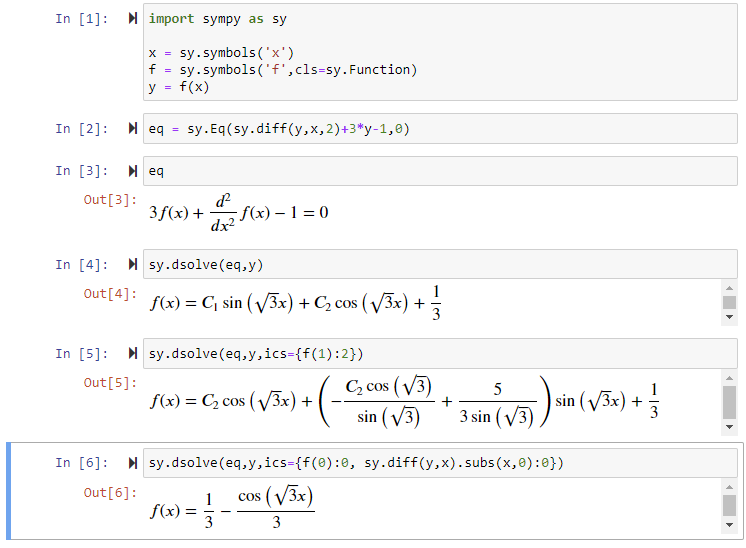
eq = sy.Eq(sy.diff(y,x,2)+3*y-1,0) # 방정식 세우기
sy.dsolve(eq,y) # (일반) 방정식 풀기
sy.dsolve(eq,y,ics={f(1):2}) # 초기 조건(1개)인 경우
sy.dsolve(eq,y,ics={f(0):0, sy.diff(y,x).subs(x,0):0}) # 초기 조건(2개)인 경우
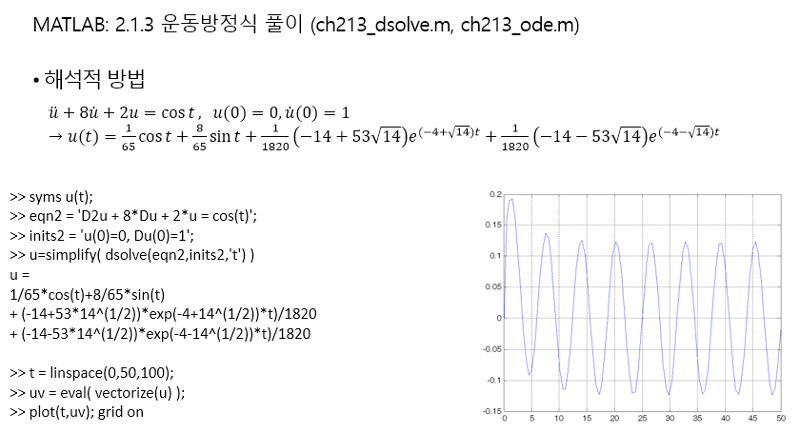
2) 2계 미분방정식(Matlab과 비교)
미분방정식(ode): u" + 8u' + 2u = cos(t)
초기 조건(ics): u(0)=0, u'(0)=1
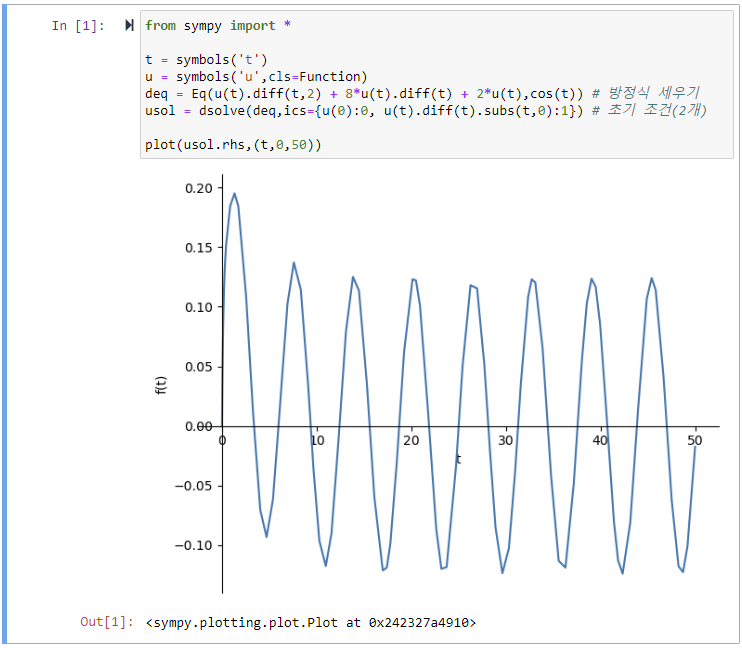
Ex)
from sympy import *
t = symbols('t')
u = symbols('u',cls=Function)
deq = Eq(u(t).diff(t,2) + 8*u(t).diff(t) + 2*u(t),cos(t)) # 방정식 세우기
usol = dsolve(deq,ics={u(0):0, u(t).diff(t).subs(t,0):1}) # 초기 조건(2개)
plot(usol.rhs,(t,0,50))
cf) grid 넣기
plot에 grid를 넣기 위해 다음 패키지를 불러들여 figure를 셋팅할 수 있다.
Ex)
import seaborn as sns
sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
(3) 방정식
1) 방정식
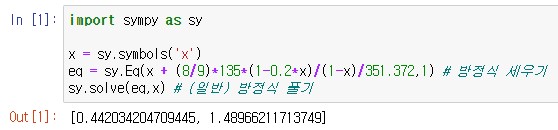
x + (8/9)*135*(1-0.2*x)/(1-x)/351.372 = 1
Ex)
import sympy as sy
x = sy.symbols('x')
eq = sy.Eq(x + (8/9)*135*(1-0.2*x)/(1-x)/351.372,1) # 방정식 세우기
sy.solve(eq,x) # (일반) 방정식 풀기
2) 연립방정식
2y + 7x = −5
5y − 7x = 12
Ex)
import sympy as sy
x,y = sy.symbols('x y', real=True)
eq1 = 2*y+7*x+5
eq2 = 5*y-7*x-12
sol = sy.solve([eq1, eq2], x, y, dict=True);sol
결과: [{x: -1, y: 1}]
