[김건우][AI 기초] 9. 선형회귀(Linear Regression) - 결정계수 & 과대, 과소적합
작성자 : 김건우
(2024-05-06)
조회수 : 11630
[YOUTUBE] https://youtu.be/SbV2qKFu4Po
[CODE] 영상 하단 설명란
|
이번시간에는 회귀 문제를 다룰텐데요. 회귀는 어떤 임의의 숫자를 예측하는 문제입니다. 저는 회귀문제를 다루기 위해서 기존의 붓꽃데이터가 아닌 물고기 데이터를 가져왔습니다. 이 물고기는 농어인데요. 농어의 길이를 통해 무게를 예측해보도록 할게요. 기존에 우리가 배운건 KNN알고리즘으로 분류를 했었죠. 정답을 0과 1로 놓았구요. 이를 타깃이라고 했습니다. 회귀는 예측하는 문제이기 때문에 분류처럼 0과 1이 타깃이 아니라 농어의 무게가 타깃이 됩니다. 가장 먼저 측정한 데이터를 확인해 봐야겠죠? x축에 길이 y축에 무게를 두고 산점도를 그려볼게요. 산점도를 통해서 우리가 알 수 있는 것은 당연하지만, 길이가 증가함에 따라 무게가 증가하는 것을 알수 있죠. 이를 통해서 두 길이와 무게 사이에는 관계가 있다고 생각을 할 수 있습니다. |
| 회귀 Regression이라는 용어는 1800년도 사람인 통계학자 프랜시스 골턴(Francis Galton)이 처음 사용했습니다. 그는 키가 큰 사람의 아이가 부모보다 더 크지 않는다는 사실을 관찰하고 이를 “평균으로 회귀한다”라고 표현했는데요. 그 후 두 변수 사이의 상관관계를 분석하는 방법을 회귀라고 정의하게 되었습니다. 수학적으로는 독립변수 x에 대응하는 종속변수 y와 가장 비슷한 값 y^를 출력하는 함수 f(x)를 찾는 과정입니다. 따라서 앞서 배웠던 분류와는 다르게 임의의 어떤 숫자를 예측하는 문제이구요. F(x)가 다음 형태의 선형함수면 이 함수를 선형회귀 모형(linear regression model)이라고 부르게 됩니다. 이 선형회귀모형을 사용하는 회귀분석을 선형회귀분석이라고 하게 되고요. 이해를 위해서 이번시간에는 1차함수부터 보도록 하겠습니다. |
|
이해보다는 우선 우리가 갖고 있는 농어의 데이터를 가지고 선형회귀모델을 바로 만들어 볼게요. 사이킷런을 사용하기 위해 데이터를 2차원배열 형태로 제공해제공 한다는 것을 기억하시나요? 2차원 배열을 위해서 우리는 인덱스를 만들고 랜덤함수로 순서를 섞어서 훈련세트와 테스트세트로 구분해서 훈련시켰었죠. 머신러닝에는 이러한 전처리 작업이 항상 필요한 작업인데요. 사이킷런에는 이러한 훈련세트와 테스트세트로 나누기 위한 도구가 이미 준비가 되어있습니다. Model_selection이라는 패키지 밑에 train_test_split 함수로 제공을 하고 있어요. 이 함수의 장점은 perch_length와 perch_weight를 한 번에 나눌 수 있어요. GPT에게 함수의 사용법과 매개변수를 한번 확인해 보겠습니다. |
| gpt에게 train_test_split 함수의 사용법과 주요 파라미터를 알려달라고 질문해 볼게요. 답변으로 기본적인 용도와 파라미터에 대해 설명을 해주고 있네요. 추가 질문을 통해 파라미터에 대해 더 자세하게 알려달라고 할수도 있어요. 간단하게 제가 알고있는 내용으로 설명을 드리면, 우리가 산점도에 그렸던 x, y값들이 각각 length와 weight인데요. 이 두개의 배열을 각각 훈련세트와 테스트세트로 나눠주어야 합니다. Length는 훈련과 테스트세트 두개로 분리하고, weight도 훈련과 테스트세트로 두개로 분리하기위해 앞에 새로운 변수명을 정의해주면 됩니다. 함수 안에는 분리할 객체인 x, y값이 들어가게 되구요. Test_size는 전체 데이터에서 나눌 비율이라고 하는데요. 지정하지 않아도 적절하게 분히라기 때문에 지정하지 않을게요. Random_state는 무작위결과를 항상 동일하게 얻기위해 고정시키는 역할입니다. 훈련 및 테스트세트 분할을 위해 인덱스에서 사용해본 적이 있어요. 마지막으로 stratify는 클래스별로 라벨을 달아주는 역할을 한다고 보면 됩니다. 주로 분류를 위해 사용되니까, 우리는 사용하지 않을겁니다. |
| 사이킷런에 사용할 데이터세트는 2차원배열이어야 하나도 제가 이야기했었는데요. Perch_length가 1차원 배열이기 때문에 이를 나눈 train_input과 test_input도 1차원 배열 형태일거에요. 이런 1차원 배열을 1개의 열이 있는 2차원 배열로 바꿔야 합니다. 기존의 분류 문제에서는 2개의 특성을 사용했기 때문에 열이 2개인 2차원 배열을 사용했는데요. 하지만 이번 데이터에서는 특성을 1개만 사용하기 때문에 수동으로 2차원 배열을 만들어 주어야 합니다. 이는 reshape( ) 메서드로 구현이 가능한데요. 바꿀 크기를 지정해주어야 합니다. 크기에 -1 이라는 숫자를 지정하게 되면 나머지 원소 개수로 모두 채우라는 의미입니다. 예를 들어 1,2,3으로 이루어진 1차원 배열에서 첫번째 크기를 나머지 원소개수로 채우고 두번째 크기를 1로 하면 크기가 기존 (3, )에서 (3, 1)로 바뀌게 될거에요. Train_input과 test_input에 이를 적용해서 2차원 배열형태로 만들어 볼게요. |
|
준비가 끝났으면 바로 fit 메서드로 선형회귀 모델을 학습시켜 보겠습니다. 이 선형회귀 모델은 직선을 학습하는데요. 학습하지 않은 50cm길이의 농어의 무게를 어떻게 예측하는지 보면 1241g으로 예측을 하네요. 만들어진 직선을 그려보고 어떻게 이런 값이 나오는지 한번 볼게요. 하나의 직선을 그리려면 기울기와 절편이 있어야 하는데요. Y = ax + b처럼 쓸 수 있겠죠. 여기선 x를 농어의 길이 y를 농어의 무게로 바꾸면 그림처럼 직선이 그려질 거에요. 처음 시작할 때 선형회귀의 수식이 복잡해 보였는데 2차원 상의 직선이라면 생각보다 단순한 형태이죠. |
|
우리가 훈련시킨 lr객체의 coef 와 intercept 속성안에 직선방정식을 찾을 수 있습니다. Lr.coef_ 와 lr.intercept_ 함수를 통해서 절편과 계수를 확인할 수 있어요. 여기서 농어의 길이 15에서 50까지 직선으로 그려볼게요. 이직선을 그리려면 앞에서 구한 기울기와 절편을 사용해서 (15, 15*39-709)와 (50, 50 * 39-709) 두점을 이으면 될겁니다. 훈련세트의 산점도와 함께 그려볼게요. 그림에서 나온 이 직선이 선형회귀 알고리즘이 이 데이터셋에서 찾은 최적의 직선입니다. 길이가 50츠인 농어에 대한 예측은 이직선의 연장선에 있죠. 조금 정리를 해보자면, 우리가 coef 와 intercept를 통해 찾은 값들은 기울기와 절편인데요. 머신러닝에서 기울기를 계수(coefficient) 또는 가중치(weight)라고 부르게 됩니다. 그리고 coef와 intercept 같은 값들은 머신러닝 알고리즘이 찾은 값이라는 의미로 모델 파라미터(model parameter)라고 부르게 됩니다. 앞으로도 계속 공부를 하겠지만, 우리가 사용할 수많은 머신러닝 알고리즘의 훈련과정은 최적의 모델 파라미터를 찾는 것과 같습니다. 이를 “모델 기반 학습” 이라고 부르게 되구요. 앞서 사용한 k-최근접 이웃에는 모델 파라미터가 없는데요. 이렇게 훈련세트를 저장하는 것이 훈련의 전부인 학습을 “사례 기반 학습” 이라고 정의하게 됩니다. |
| 이제 모델을 생성했으니 score 메서드로 훈련세트와 테스트세트에대한 정확도도 확인을 해봐야겠죠. 훈련세트에서 정확도가 93%, 테스트 세트에서 82%가 나왔는데요. 두 데이터세트 사이의 차이가 많이 나게 되죠. 이 차이에 대해서 우리가 고민을 해보기 전에 한번 회귀에서의 정확도는 무엇을 의미하는지 한번 생각해 봤으면 좋겠는데요. k최근접이웃 같은 분류알고리즘에서는 두 클래스의 분류를 정확히 분류했냐 안했냐로 정확도를 출력했습니다. 그렇다면 회귀에서는 직선을 학습했는데 과연 무엇에 대한 정확도일까요? |
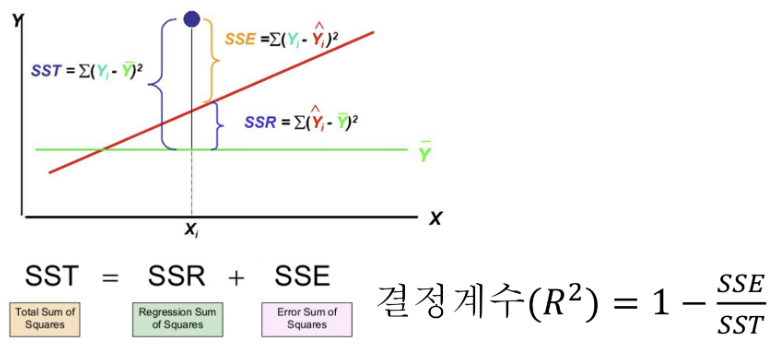
| 머신러닝에서 정확도는 결국 학습한 모델을 평가하는 지표일텐데요. 이를 위해서 사용하는 개념이 결정계수(R^2) 이라는 것이 있어요. 결정계수는 추정한 선형 모형이 주어진 자료에 얼마나 적합한지 정도를 재는 척도라고 할수 있는데요. 다르게 이야기하면 독립변수에서 예측가능한 종속 변수의 변동 비율입니다. 수식으로 보면 0과 1사이의 값으로 나오는 값이고, 분모가 크다면 1에 가까워져 흔히 말하는 정확도가 높아진다는 것을 의미하겠죠. 분자에는 각 샘플의 타깃과 예측한 값의 차이를 제곱하여 더해주고요. 타깃과 타깃 평균의 차이를 제곱하여 더한 값을 분모로 들어가 나눠줍니다. 만약 타깃의 평균 정도를 예측하는 수준이라면, 즉 분자와 분모가 비슷해져서 결정계수는 0에 가까워 질것이구. 예측이 타깃에 아주 가까워지면 분자가 0에 가까워지기 때문에 1에 가까운 값이 될것입니다. 직감적으로 이 결정계수가 얼마나 좋은지 이해하기 어려울 수 있는데요. 언젠가는 이해하기를 바랄게요. 결정계수 말고도 다른 값으로도 계산할 수 있는데요. “평균 절댓값 오차(mean absolute error)”를 이용하면 타깃과 예측한 값사이의 차이가 어느정도 예측에서 벗어났는지 가늠하기 좋아요. 결과를 보면 95g 정도 농어의 무게와 다르다는 것을 알수 있는데요. 이정도의 수치면 좀전에 테스트 세트에서 82%라는 결정계수 값이 조금 이해가 되네요. 결국 결정계수라는 것은 항상 결과 변수의 평균을 예측하는 모델과 비교하여 모델이 데이터를 예측하는데 얼마나 좋은지 0과 1사이의 척도에서 알려주는 비교 지표라고 할 수 있습니다. 이외에도 사이킷런에는 여러가지 평가지표들이 있는데요. 선형회귀는 이정도로 충분 하구요. 다른 알고리즘에서 기회가 되면 더 보도록 하겠습니다. |
|
이제 우리가 score 메서드로 출력되는 값의 의미도 이해를 했으니까요. 테스트세트에서 좋지 않은 결과가 나왔다는 것을 이해했죠. 우리가 만든 결과처럼 훈련세트에서 점수가 높고 테스트세트에서 과도하게 점수가 낮은 경우를 “과대적합”이라고 이야기합니다. 그와 반대되는 경우는 과소적합이라고 이야기를 하구요. 오늘은 용어가 많이 등장을 하네요. 다시 이야기를 하자면, 훈련세트에서 점수가 굉장히 좋았는데 테스트 세트에서는 점수가 굉장히 나쁘다면 훈련세트에 모델이 과대적합 이라고 이야기 하는데요. 즉 훈련 세트에만 잘 맞는 모델이라 테스트 세트를 가지고 시험해서 새로운 샘플에 대한 예측을 만들 때 잘 동작하지 않을 겁니다. 반대로 훈련세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 낮은 경우는 어떨까요? 이런 경우를 모델이 훈련세트에 과소적합 되었다고 이야기 하는데요. 모델이 너무 단순해서 훈련세트에서 적절히 훈련되지 않은 경우입니다. 훈련세트가 전체 데이터를 대표한다고 가정하기 때문에 훈련세트를 잘 학습하는 것이 중요해요. 이런 과소적합의 또 다른 원인은 훈련세트와 테스트세트의 크기가 매우 작기 때문인데요. 데이터가 작으면 테스트세트가 훈련세트의 특징을 따르지 못할 수 있어요. 이를 해결하기 위해서 과대적합의 경우에는 모델을 단순화시키는게 해결책이 될수 있구요. 과소적합의 경우에는 모델을 복잡하게 만들면 되요. 다시 돌아와서 결과를 한번 보겠습니다. 훈련세트에서 결정계수 값이 0.93, 테스트세트에서 0.82가 나왔죠. 전형적인 과대적합이라고 과연 말할 수 있을까요? 사실 이런경우에는 훈련세트의 점수도 그렇게 높다고 할 수 없습니다. 오히려 전체적으로 과소적합 되었다고 볼 수 있어요. 과소적합 말고도 또 다른 문제가 있죠. 그래프 왼쪽 아래를 보면 뭔가 이상하죠. 이를 해결하기 위해 직선이 아닌 다항식을 이용한 회귀 곡선을 만들 수 있을 것 같네요. |
